Solução:

1. a)
   ​

   A seção meridiana é a interseção do cilindro com um plano que contém seu eixo. Se este plano, digamos $\alpha$ contém o eixo do cilindro, então intersecta as bases do cilindro em diâmetros. Estes diâmetros são coplanares pois ambos estão em $\alpha$, logo os diâmetros precisam ser paralelos pois estão contidos nos planos das bases, que são paralelos. Como o plano $\alpha$ contém o eixo do cilindro, ele intersecta a superfície lateral do cilindro em duas gerarizes pois elas são paralelas ao eixo e, portanto, paralelas entre si. Como os lados opostos deste quadrilátero são paralelos, o quadrilátero é um paralelogramo.

2. b)
   ​

   Toda seção meridiana é determinada pelo eixo central do cilindro e por um diâmetro do círculo da base. Seus lados são um diâmetro de cada base e duas geratrizes do clindro que possuem extremidades nesses diâmetros. Como as geratrizes são paralelas ao eixo central do cilindro, a seção meridiana será um retângulo quando o eixo central e o diâmetro forem perpendiculares. Este é sempre o caso quando o cilndro é reto. Se o cilindro for oblíquo, sejam $O$ e $O^{\prime}$ os centros dos círculos das bases do cilindro, $\alpha$ o plano que contém $O$ e uma das bases do cilindro e $O^{\prime\prime}$ a projeção ortogonal de $O^{\prime}$ em $\alpha$, $r$ a reta contida no plano $\alpha$ que é perpendicular a $OO^{\prime\prime}$ e que passa em $O$.

   

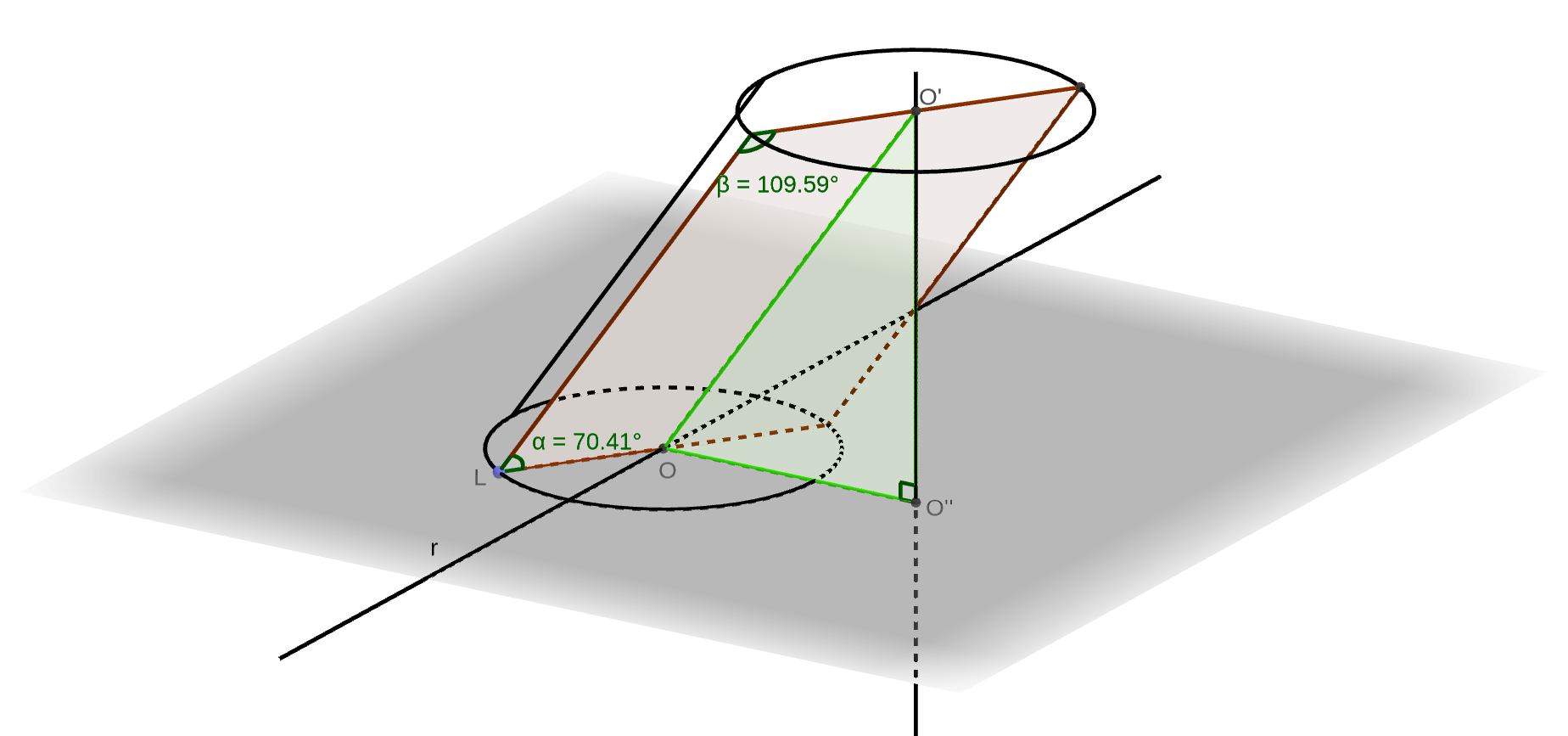
   Como $O^{\prime\prime}$ é a projeção ortogonal de $O^{\prime}$ em $\alpha$, a reta $O^{\prime}O^{\prime\prime}$ é perpendicular ao plano $\alpha$, logo é perpendicular (ortogonal) a $r$. Então $r$ é perpendicular ao plano $OO^{\prime}O^{\prime\prime}$ pois é perpendicular às retas concorrentes $OO^{\prime\prime}$ e $O^{\prime}O^{\prime\prime}$. Como $r$ é perpendicular ao plano $OO^{\prime}O^{\prime\prime}$, é perpendicular à reta $OO^{\prime}$. Portanto, o diâmetro do círculo da base de $\alpha$ que torna a seção meridiana um paralelogramo é aquele que está contido em $r$.

Resolva os exercícios 7, 8, 14, 15 e 17 da aula 24 do módulo da disciplina. Solução: As soluções estão no gabarito do módulo, disponível na sala da disciplina.