Geometria Espacial - EP Aula 22 - Gabarito
Exercício 1.
Qual é o polígono com o maior número de lados que se pode obter como interseção de um cubo e um plano? Faça uma figura que represente a sua resposta.
Solução: Como o cubo possui 6 lados, uma primeira limitação para este número é 6. Experimentando você pode encontrar uma seção como a da figura abaixo com exatamente 6 lados. Neste caso os vértices do polígono são pontos médios das arestas, mas isso não é necessário para se obter um hexágono. Veja este aplicativo: https://www.geogebra.org/m/axjppyqr
Exercício 2.
A soma total dos ângulos de todas as faces de um prisma é 8640. Quantos lados tem o polígono de base?
Solução: Lembrando que a soma dos ângulos internos de um polígono de lados é e que a soma dos ângulos internos de um quadrilátero é , temos que a soma dos ângulos internos de todas as faces de um prisma cujo polígono de base tem lados é dada por . Como , temos após poucas contas que .
Exercício 3.
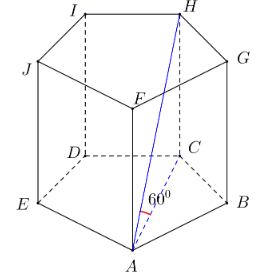
Um prisma reto cuja base é um pentágono regular de lado medindo 1 cm tem uma diagonal maior fazendo ângulo de 60 com o plano da base. Determine a área lateral do prisma.
Solução: A diagonal do pentágono de base mede (veja o apêndice). Como é a projeção ortogonal de sobre o plano da base e a diagonal do prisma faz ângulo de com o plano da base, o ângulo entre e é . Finalmente, como o prisma é reto, o triângulo é retângulo em e portanto , logo . Então a área lateral deste prisma reto é .
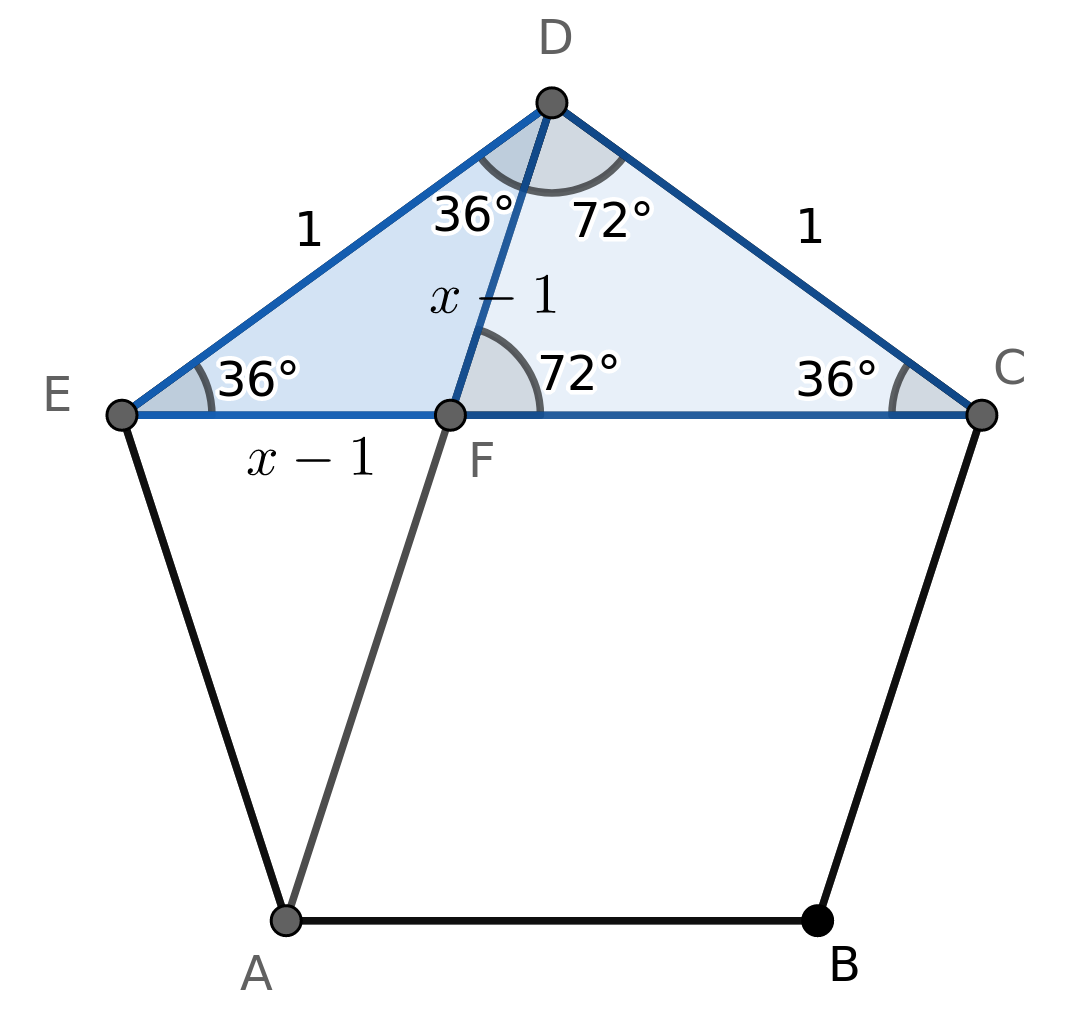
Apêndice à solução: Seja o comprimento da diagonal de um pentágono regular de lado 1. Lembre-se que o ângulo interno de um pentágono regular é 108. Na figura, os triângulos , e são isósceles e e são semelhantes pelo caso ângulo-ângulo. Então temos , ou seja, , logo .
Observação: Acredito que as contas deste apêndice sejam importantes para estarem presentes no “repertório” de um Professor de Matemática do Ensino Médio ou de cursos preparatórios desse nível de escolaridade.
Exercício 4.
Por duas vezes Benício juntou, como na figura, três dados com faces numeradas de 1 a 6, de tal modo que faces em contato tivessem o mesmo número. Em cada uma das vezes ele somou os números de todas as faces que não ficaram em contato entre si. A diferença entre as somas obtidas foi 16. Quais são os números das faces que nunca ficaram em contato entre si?
Solução: Esta questão tem por objetivo desenvolver um pouco da visão espacial do estudante e estimular o raciocínio lógico.
Sejam e as somas das faces que não estão em contato em cada uma das vezes que Benício juntou os dados. Umas das técnicas de resolução de problemas mais conhecidas é trabalhar com o complementar: em vez de tentar determinar as faces que somamos, vamos considerar aquelas que estão em contato. Como a soma de todas as faces de um dado é , os valores de e de são dados por 63 menos as faces que estão em contato. Digamos que na primeira montagem as faces que estão em contato são e , então . Analogamente , onde e são as faces que ficaram em contato.
Não há perda de generalidade em supor que e neste caso sabe-se do enunciado que . Isto equivale a . Como , , e são faces de dados e como e , temos
Uma análise caso a caso nos mostra que e (ou e ) e e (ou e ). Observe que as montagens com os valores entre parênteses são as mesmas das que estão fora pois podem ser obtidas daquelas por uma rotação.
Em todo caso, as faces que não estão em contato em nenhuma das duas montagens são as faces 3 e 4.
Uma solução mais curta para este problema pode ser encontrada na questão 12 da OBMEP 2017 neste vídeo.
Exercício 5.
Existe algum prisma em que uma das faces laterais pode ser tomada por base do prisma? Justifique a sua resposta.
Solução: Sim, os paralelepípedos são prismas em que qualquer face pode ser tomada por base. De fato, escolha uma face de um paralelepípedo, por definição, todas as faces adjacentes a são paralelogramos. Além disso, conforme provado na Proposição 2 desta aula a face oposta a é paralela e congruente a ela.
Exercício 6.
Mostre que as faces opostas de um paralelepípedo são paralelas e congruentes.
Solução: Esta é a proposição 2 desta aula.
Exercício 7.
Considere um cubo de aresta 40cm apoiado sobre a face , tomada por base do prisma. Imagine que a ponta de um barbante foi colada no vértice , o barbante deu duas voltas em torno do cubo, cruzando as faces laterais e a outra ponta foi colada no vértice .
-
a)
Faça uma figura ilustrativa que represente a situação.
-
b)
Calcule o menor comprimento possível do barbante em questão. Apresente o seu raciocínio.
Solução:
-
a)
-
b)
Em cada uma das faces, o comprimento dos segmentos vermelhos que representam trechos do barbante são coincidem com seus comprimentos na planificação. Na planificação o menor caminho entre os pontos e cruzando todas as faces laterais duas vezes é a união dos segmentos de reta indicados na figura.
Portanto, chamando de a aresta do cubo, o comprimento do barbante é a soma das hipotenusas dos triângulos retângulos (congruentes) destacados na figura. Usando o Teorema de Pitágoras obtemos