Geometria Espacial - EP Aula 21 - Gabarito
Aula 21: Ângulos no espaço - parte II
Exercício 1.
Decida se as afirmações a seguir são verdadeiras ou falsas. Prove as verdadeiras e encontre um contra-exemplo para as falsas (este contra-exemplo deve ser descrito e desenhado).
-
a)
Sejam um plano e uma reta. Se é oblíqua a , então o ângulo entre e é igual ao ângulo entre e .
-
b)
Se duas retas distintas são paralelas a um plano, então elas são paralelas entre si.
Solução:
-
a)
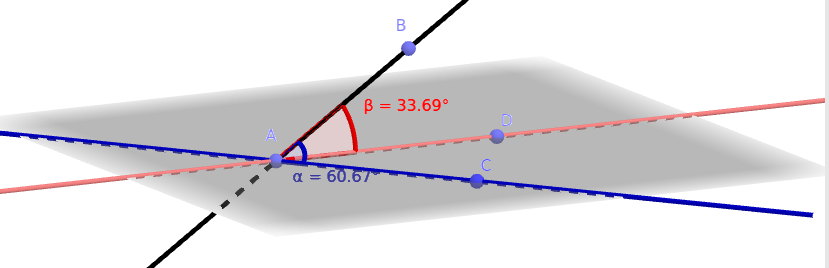
Falso. O ângulo entre uma reta oblíqua a um plano e o plano é o ângulo entre a reta e sua projeção ortogonal no plano. Este é o menor ângulo entre uma reta do plano e a reta dada. Veja o exemplo da figura abaixo. Ela pode ser manipulada no Geogebra neste link11 1 https://ggbm.at/RSsBdrCp e você pode encontrar uma explicação visual a partir de manipulação no Geogebra no vídeo da semana neste link22 2 https://www.youtube.com/watch?v=Mu8hugp8S_4.
-
b)
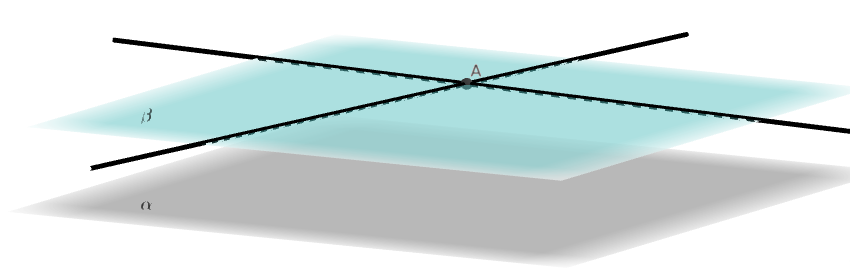
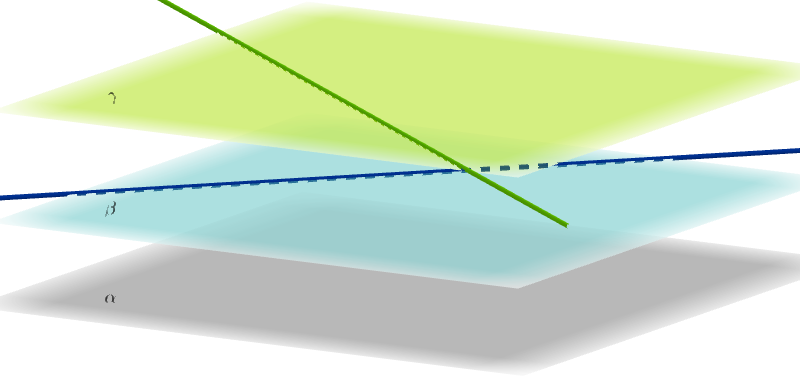
Falso. Considere, por exemplo, duas retas concorrentes contidas num plano paralelo ao plano . Ambas são paralelas a , mas não são paralelas entre si. Tomando três planos paralelos, podemos obter duas retas reversas, ambas paraslelas a . Veja as figuras.
Exercício 2.
Seja um plano e uma reta. Quantos planos contendo perpendiculares a existem nas condições a seguir? Justifique sua resposta.
-
a)
A reta está contida em .
-
b)
A reta é paralela a .
-
c)
A reta é secante, mas não é perpendicular a .
-
d)
A reta é perpendicular a .
Solução: As respostas e as justificativas para os itens a), b) e c) são as mesmas. Para evitar confusão, apresentamos uma figura para cada item.
-
a)
Apenas um plano. Seja e a única reta perpendicular a por (a existência e a unicidade da reta são garantidas pela Proposição 8 da Aula 20). Como não é perpendicular a , as retas e são concorrentes, logo determinam um plano, digamos (Proposição 1 da Aula 18). Como o plano contém a reta , que é perpendicular a , os planos e são perpendiculares (Proposição 1 da Aula 21). Falta mostrar que o plano é o único plano perpendicular a que contém . Seja um plano perpendicular a que contém . Vamos mostrar que . Como e são perpendiculares a , a Proposição 2 da Aula 21 garante que está contida em ou é paralela a . A reta não pode ser paralela a pois ela contém o , portanto, está contida em . Lembre-se que duas retas concorrentes determinam um único plano (Proposição 1 da Aula 18) e os planos e contêm as retas concorrentes e , logo .
-
b)
Resolvido no item a).
-
c)
Resolvido no item a).
-
d)
Existem infinitos planos. Se a reta é perpendicular ao plano , então qualquer plano que contenha será perpendicular a (esta é a Proposição 1 da Aula 21). Por outro lado, existem infinitos planos que contêm a reta , qualquer que seja a reta (esse é um exercício do EP da Aula 18).
Exercício 3.
O aplicativo exibe uma pirâmide regular de vértice , base hexágono de lado 1 cm e arestas laterais com medida 2 cm. O ponto é médio da aresta lateral .
-
a)
Use o aplicativo para obter os ângulos , , , , e .
-
b)
Determine o ângulo entre e o plano , da base da pirâmide.
Solução:
-
a)
Basta mover o ponto vermelho no aplicativo e anotar os resultados que são aproximadamente , , , , e .
-
b)
O ângulo entre uma reta e um plano é o ângulo entre a reta e sua projeção ortogonal no plano em questão. Neste caso, como o plano é perpendicular ao plano da base, o ângulo é o ângulo .
Exercício 4.
A figura representa um tetraedro regular de aresta 2 cm.
-
a)
Calcule o ângulo entre a aresta e a face do tetraedro.
-
b)
Calcule o ângulo entre duas faces do tetraedro.
Solução:
O ângulo entre uma reta e um plano é o ângulo entre a reta e sua projeção ortogonal sobre o plano em questão. A projeção ortogonal de sobre é a reta , onde é a projeção ortogonal de sobre .
Afirmação: a projeção ortogonal de sobre é o baricentro do triângulo .
De fato, se é o pé da perpendicular baixada de sobre o plano , então a reta é perpendicular ao plano e, portanto, perpendicular a , e a . Para mostrar que é o baricentro do triângulo equilátero , basta mostrar que é equidistante de , e , isto é, que . Para concluir este fato basta observar que os triângulos retângulos , e possuem hipotenusas de mesmo comprimento e o cateto coincidentes, então são congruentes, logo .
A projeção ortogonal da reta sobre o plano é a reta , onde é o ponto médio de . Agora basta calcular o ângulo usando a Lei dos Cossenos no triângulo .
De onde, lembrando que o triângulo é isósceles de base e que é altura do triângulo equilátero obtemos,
Assim, o ângulo procurado é o ângulo entre zero e cujo cosseno é . Este ângulo é de aproximadamente
Exercício 5.
Um cubo de lado foi secionado pelos planos e e as pirâmides e foram retiradas.
-
a)
Faça uma figura que ilustre o sólido restante, use transparência para que se possa ver o outro lado.
-
b)
Calcule o ângulo entre as faces e deste novo sólido.
Solução:
-
a)
O sólido obtido tem como arestas a figura a seguir. Se preferir uma visualização tridimensional no GeoGebra, acesse este link 33 3 https://www.geogebra.org/m/qmhcfmzv.
-
b)
Lembre-se que o ângulo entre dois planos é o ângulo entre duas retas contidas nos respectivos planos e ambas perpendiculares à reta de interseção dos dois planos (essas retas são as interseções do plano perpendicular à reta de interseção com os planos que se quer calcular o ângulo, veja a definição na Aula 21). Como os triângulos e são equiláteros, as medianas partindo de e são perpendiculares à base desses triângulos e podem ser usadas para calcular o ângulo entre os planos. Seja o ponto médio da aresta . O ângulo procurado é o ângulo entre as retas e .
Usando a Lei dos Cossenos no triângulo obtemos
Os segmentos e são alturas relativas à dos triângulos equiláteros e de lados , respectivamente. Portanto, , que também pode ser obtido usando-se o Teorema de Pitágoras duas vezes. Substituindo na Lei dos Cossenos obtemos .
Observe que o tetraedro de vértices possui todas as arestas iguais (congruentes). O ângulo calculado é o ângulo entre duas faces de um tetraedro regular.
Exercício 6.
Seja um quadrilátero convexo cuja interseção com o plano é vazia. Seja a projeção ortogonal de sobre . Qual(is) hipótese(s) deve(m) ser adicionada(s) para que e sejam congruentes? Justifique a sua solução.
Solução: O quadrilátero deve estar contido num plano paralelo a . Pois assim os ângulos entre os lados e comprimentos dos lados de serão preservados no quadrilátero projetado .
Exercício 7.
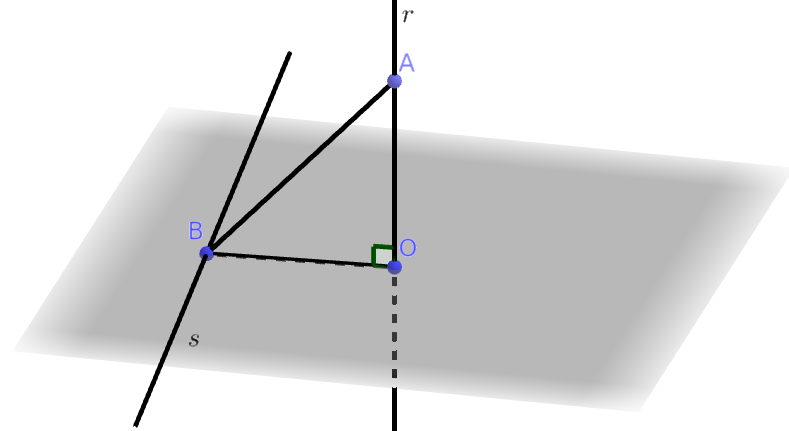
Considere um plano , uma reta perpendicular a no ponto e uma reta que não contém . Se é um ponto em e um ponto em , mostre que é perpendicular a se, e somente se, é perpendicular a .
Solução:
A primeira coisa a se fazer é tentar visualizar a figura do enunciado.
Lembre-se que uma proposição do tipo se, e somente se, contém duas duas proposições: “Se , então ” e outra “Se , então ”. Neste caso precisamos justificar as duas afirmações.
Afirmação 1: Se é perpendicular a , então é perpendicular a .
Afirmação 2: Se é perpendicular a , então é perpendicular a .
Uma boa estratégia para se verificar o perpendicularismo entre duas retas é mostrar que existe um plano que contém uma delas e é perpendicular à outra.
Lembre-se que uma reta perpendicular a um plano é uma reta perpendicular a todas as retas deste plano (esta é a definição). Mas para fins práticos podemos usar o teorema que afirma que: se uma reta é perpendicular a duas retas concorrentes de um plano, então ela é perpendicular ao plano.
Passemos a justificar as afirmações:
Justificativa da Afirmação 1: Se é perpendicular a , então temos e perpendiculares a . Como e são concorrentes, a reta é perpendicular ao plano , determinado por e . Como é perpendicular ao plano , é perpendicular a todas as retas de , em particular, é perpendicular a .
Justificativa da Afirmação 2: Se é perpendicular a , então temos e perpendiculares a . Como e são concorrentes, a reta é perpendicular ao plano , determinado por e . Como é perpendicular ao plano , é perpendicular a todas as retas de , em particular, é perpendicular a .