Exercício 1.

Geometria Espacial - Exercícios Programados da Aula 20: Ângulos no espaço¹¹ 1 O conteúdo desta semana encontra-se no livro Geometria Básica - Volume 2. - Gabarito

Exercício 1.

Verifique se as afirmações abaixo são verdadeiras ou falsas. Ilustre com um exemplo as verdadeiras e com um contra-exemplo as falsas.

a)

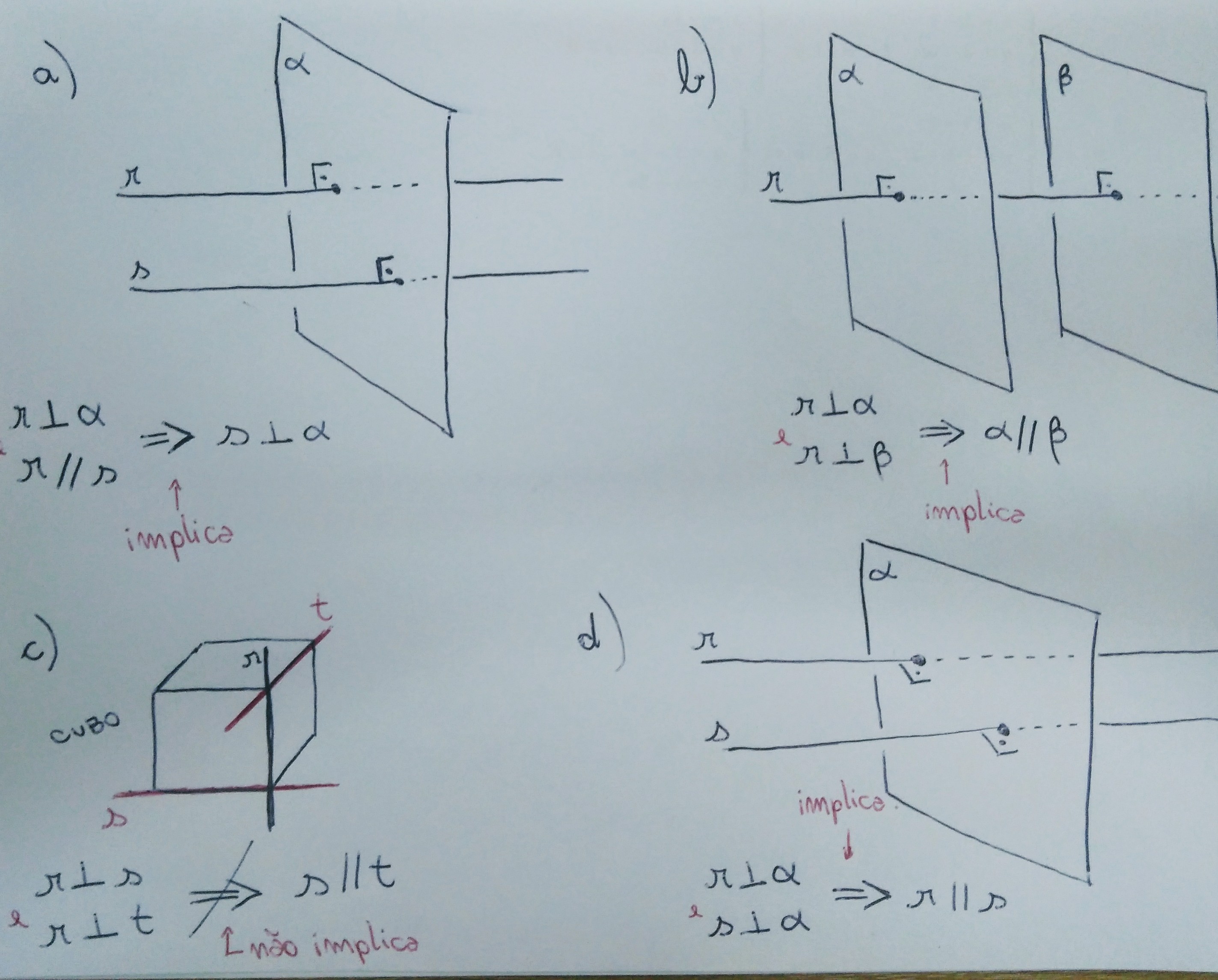
Se duas retas são paralelas entre si e um plano é perpendicular a uma delas, então ele é perpendicular à outra reta.
b)

Se dois planos distintos são perpendiculares a uma reta, então eles são paralelos entre si.
c)

Se duas retas distintas são perpendiculares a uma reta do espaço, então elas são paralelas.
d)

Se duas retas distintas são perpendiculares a um plano, então elas são paralelas.

Solução:

a)

Verdadeiro.
b)

Verdadeiro.
c)

Falso.
d)

Verdadeiro.

Ilustrações:

Exercício 2.

Seja $\alpha$ um plano e $r$ uma reta não perpendicular a $\alpha$ . Quantos planos contendo $r$ perpendiculares a $\alpha$ existem? Justifique sua resposta.

Solução: Apenas um plano. Seja $P$ , a interseção de $r$ com $\alpha$ . Sabemos que existe uma única reta perpendicular a $\alpha$ passando por $P$ e que esta reta está contida em qualquer plano perpendicular a $\alpha$ que passe por $P$ . Logo qualquer plano perpendicular a $\alpha$ que contenha $r$ , também contém a reta $s$ . Logo o plano procurado é o único plano que contém as retas concorrentes $r$ e $s$ .

Exercício 3.

A figura a seguir representa um cubo de aresta $1$ . Mostre que as retas $EC$ e $BD$ são perpendiculares.

Solução: Uma boa estratégia para se verificar que duas retas são perpendiculares é encontrar um plano que contenha uma delas e seja perpendicular à outra. Aqui o plano $AEC$ contém a reta $EC$ e é perpendicular à reta $BD$ . De fato, $BD$ é perpendicular às retas concorrentes $AE$ e $AC$ , ambas contidas em $AEC$ , logo $BD$ é perpendicular ao plano $AEC$ . Assim, $BD$ é perpendicular a todas as retas do plano $AEC$ , portanto, $BD$ é perpendicular a $EC$ .

Definição 1.

Dados dois pontos $A$ e $B$ no espaço, o plano mediador do segmento $AB$ é o plano perpendicular ao segmento $AB$ que passa pelo ponto médio de $AB$ .

Exercício 4.

O plano mediador $\mu_{AB}$ de um segmento $AB$ cumpre, no espaço, o papel que a mediatriz cumpre no plano no sentido de que ele é o conjunto dos pontos do espaço que estão a uma mesma distância dos extremos do segmento. Nesta questão você deverá justificar este fato.

a)

Considere um ponto $P$ do plano mediador do segmento $AB$ . Mostre que $PA=PB$ .
b)

Seja $Q$ um ponto do espaço tal que $QA=QB$ . Mostre que $Q$ pertence ao plano mediador do segmento $AB$ .
c)

Conclua dos itens a) e b) que o plano mediador $\mu_{AB}$ do segmento $AB$ é o conjunto

$\mu_{AB}=\{X\;/\;XA=XB\}.$

Solução:

a)

Seja $M$ o ponto médio do segmento $AB$ . Como $AB$ é perpendicular ao plano $\mu_{AB}$ , então $AB$ é perpendicular a toda reta deste plano. Em particular, $AB$ é perpendicular a $PM$ . Portanto, a reta $PM$ é perpendicular ao segmento $AB$ e passa pelo ponto médio de $AB$ , ou seja, a reta $PM$ é a mediatriz do segmento $AB$ no plano $PAB$ . Logo, $PA=PB$ .

De outro modo, pode-se justificar que os triângulos $PAM$ e $PBM$ são congruentes pelo caso LAL de congruência de triângulos pois $AM=BM$ , $\widehat{AMP}=\widehat{BMP}=90^{\circ}$ e $PM$ é comum a ambos os triângulos, logo $PA=PB$ .
b)

Considere o plano $QAB$ . Como os pontos $A$ e $B$ pertencem a este plano, a reta $AB$ está contida nele. Logo, o ponto médio $M$ de $AB$ também pertence ao plano $QAB$ . Assim o resultado novamente segue do caso plano, pois se $QA=QB$ , então $Q$ pertence à mediatriz do segmento $AB$ no plano $QAB$ e, portanto, a reta $QM$ é perpendicular a $AB$ . Conclusão, $Q$ pertence ao plano mediador de $AB$ .

Caso prefira evitar usar a propriedade da mediatriz como lugar geométrico, pode-se observar que os triângulos $QAM$ e $QBM$ , do plano $QAB$ são congruentes pelo caso $LLL$ de congruência de triângulos, donde os ângulos $QMA$ e $QMB$ são iguais e somam $180^{\circ}$ , logo são ângulos retos, de onde conclui-se que $Q$ pertence ao plano mediador de $AB$ .
c)

Justificamos no item a) que todo ponto do plano mediador cumpre a condição $PA=PB$ , isto é, que

$\mu_{AB}\subset\{X\;/\;XA=XB\}.$

No item b) mostramos que todo ponto $Q$ do espaço que satisfaz $QA=QB$ é um ponto do plano mediador, isto é, mostramos que

$\mu_{AB}\supset\{X\;/\;XA=XB\}.$

Isso significa que os conjuntos $\mu_{AB}$ e $\{X\;/\;XA=XB\}$ têm exatamente os mesmos elementos, ou seja, são conjuntos iguais.

Exercício 5.

A figura representa um octaedro regular de vértices $A$ , $B$ , $C$ , $D$ , $E$ e $F$ . Um octaedro regular é um sólido geométrico que possui 8 faces, que são todas triângulos equiláteros. Mostre que os vértices $A$ , $B$ , $C$ e $D$ estão todos no mesmo plano e conclua que $ABCD$ é um losango.

Solução: Observe que $AE=AF$ , logo do Exercício 4, obtemos que $A$ pertence ao plano mediador do segmento $EF$ . Do mesmo modo, $BE=BF$ , logo $B\in\mu_{EF}$ . Analogamente, temos que $C$ e $D$ são pontos de $\mu_{EF}$ . Assim, todos os pontos $A$ , $B$ , $C$ e $D$ pertencem ao plano $\mu_{EF}$ , logo são coplanares. Portanto, a linha poligonal $ABCD$ é um polígono plano com todos os lados iguais, logo $ABCD$ é um losango.

Exercício 6.

Mostre que a reta $EF$ é perpendicular ao plano $ABC$ .

Solução: Como os polígonos $ABCD$ , $AECF$ e $BFDE$ são losangos (polígono plano com todos os lados iguais), o segmento $EF$ é perpendicular às retas concorrentes $AC$ e $BD$ do plano $ABC$ . Logo $EF$ é perpendicular ao plano $ABC$ (Proposição 2 da Aula 20).

Exercício 7.

No cubo da figura os pontos $M$ , $N$ , $O$ , $P$ , $Q$ e $R$ são pontos médios das arestas $AB$ , $BF$ , $FG$ , $GH$ , $HD$ e $DA$ , respectivamente (veja a figura). Mostre que os pontos $M$ , $N$ , $O$ , $P$ , $Q$ e $R$ estão todos num mesmo plano.

Solução: Todos os pontos azuis estão no plano mediador do segmento $EC$ pois estão à mesma distância de $E$ e de $C$ (veja a Questão 2). De fato, observe que para $X\in\{M,N,O,P,Q,R\}$ temos que tanto $EX$ como $CX$ são hipotenusas de triângulos retângulos com catetos de medidas iguais ao lado do cubo e à metade do lado do cubo. Portanto, $EX=CX$ . A figura a seguir ilustra a situação em que $X=N$ . Os triângulos $EFN$ e $CBN$ são retângulos e possuem catetos respectivamente congruentes, logo as hipotenusas $EN$ e $CN$ são iguais. Os outros casos são inteiramente análogos.