Geometria Espacial - EP Aula 19 - Gabarito
Definição: Dizemos que dois planos são paralelos quando a interseção entre eles é vazia.
Exercício 1.
A afirmação a seguir é falsa. “Se um plano contém duas retas paralelas a outro plano, então estes dois planos são paralelos.”
-
a)
Apresente um contra-exemplo com uma figura bastante ilustrativa.
-
b)
Discuta que alteração deve ser feita na afirmação para corrigi-la.
Solução:
-
a)
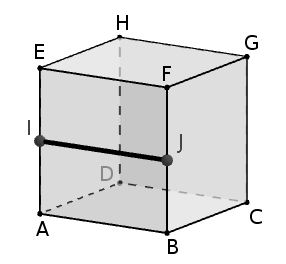
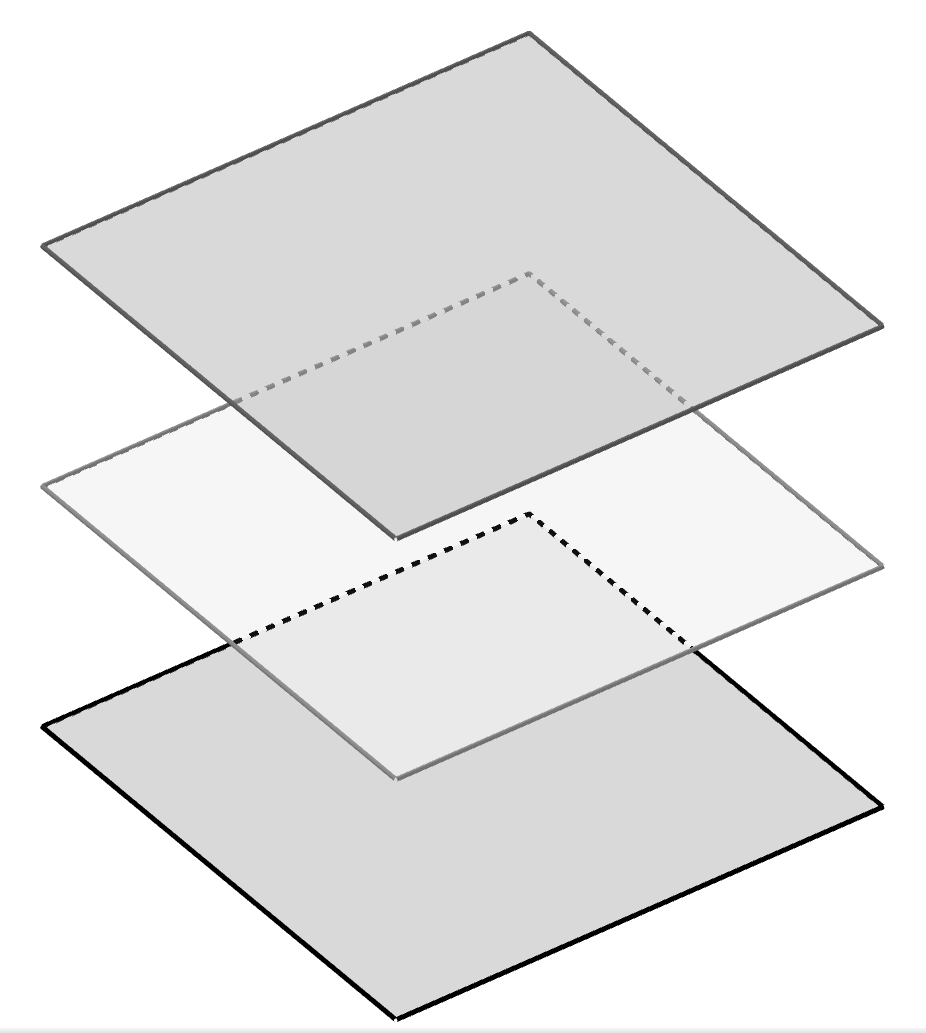
A figura representa um cubo . Os pontos e são médios das arestas e , respectivamente. Portanto, as retas e do plano são paralelas ao plano pois são paralelas à reta , mas os planos e não são paralelos. Isto é possível porque as retas e são paralelas.
-
b)
A afirmação torna-se correta quando adicionamos a hipótese de que as retas são concorrentes. Portanto, a afirmação certa é: “Se um plano contém duas retas concorrentes que são paralelas a outro plano, então estes dois planos são paralelos.”
Exercício 2.
A seguir são apresentadas afirmações e justificativas para as mesmas sobre o cubo da figura. Decida se as justificativas são válidas ou não. Corrija as justificativas erradas.
-
a)
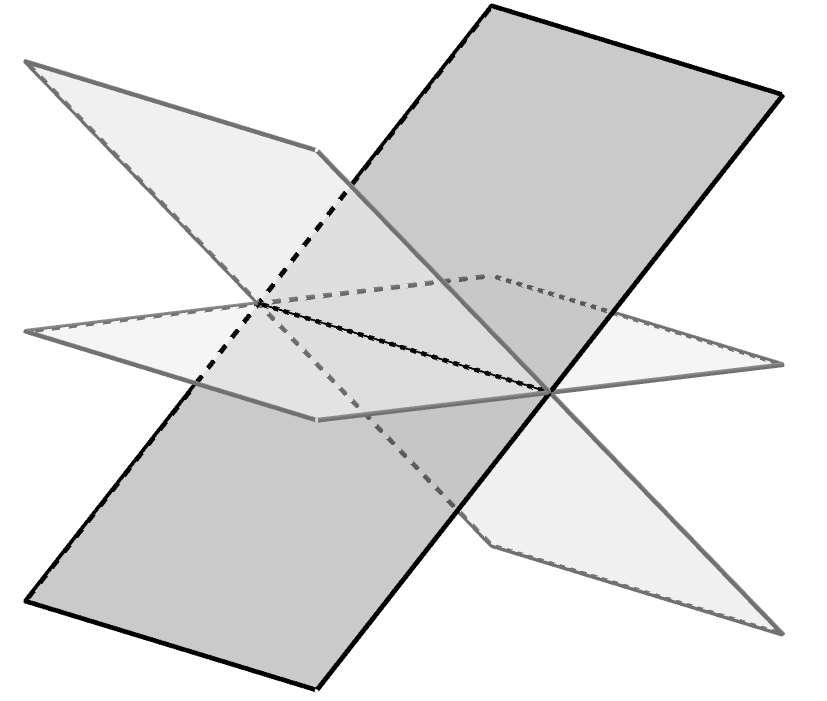
Os planos e são paralelos porque as faces e do cubo não se intersectam, isto é, as faces não têm pontos em comum.
-
b)
Os planos e são paralelos porque as retas e são paralelas, já que é um quadrado. Se um plano contém uma reta paralela a outro plano, então esses planos são paralelos.
Solução: Todas as afirmações são verdadeiras, mas algumas justificativas não estão corretas.
-
a)
As faces do cubo são quadrados contidos nos respectivos planos. Os planos são ilimitados em todas as direções, portanto, os planos poderiam se intersectar, mesmo que não se intersectem nos quadrados. Para mostrar que os dois planos são paralelos é suficiente mostrar que existem retas concorrentes em um deles que são, respectivamente, paralelas a um par de retas concorrentes do outro plano. Por exemplo, Como as faces são quadrados, basta observar que e são concorrentes em e é paralela a e é paralela a , como e são concorrentes e ambas estão contidas no plano , segue que os planos e são paralelos.
-
b)
Novamente a justificativa não basta para se obter o resultado desejado. Conforme observado no item anterior, não basta uma reta em um plano ser paralela ao outro plano para que os planos sejam paralelas. São necessárias duas retas concorrentes. Reflita sobre isso!
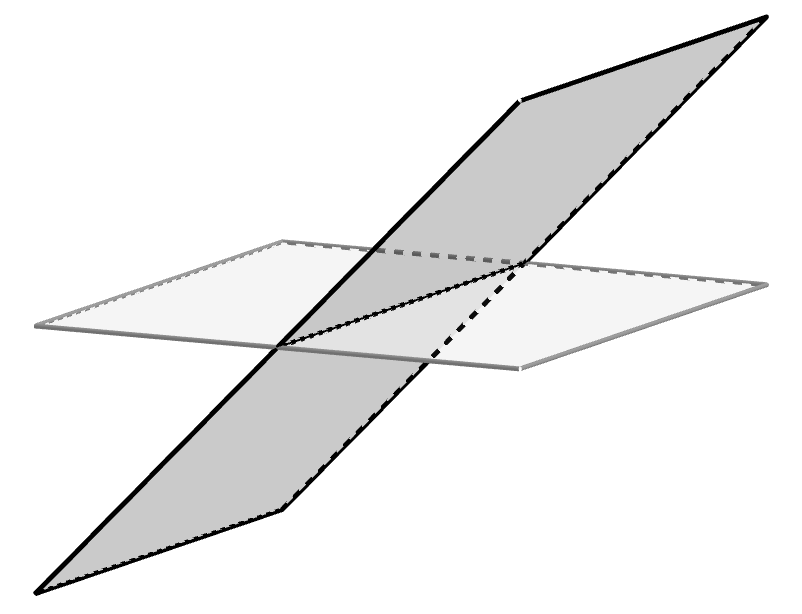
Lembre-se que dois planos no espaço podem ser secantes, paralelos ou coincidentes (quando são iguais). Estas são as posições relativas de dois pontos com relação à natureza da interseção dos planos.
Exercício 3.
Complete a tabela a seguir com as oito posições relativas de três planos, digamos , e , no espaço tridimensional com relação às interseções dois a dois e dos três planos.
Explique com as suas palavras por que estas são todas as posições relativas com relação às interseções.
Solução:
A argumentação se baseia no fato de que existem exatamente três posições relativas possíveis para dois planos no espaço tridimensional e que também são 3 as posições possíveis de uma reta e um plano. Há três posições possíveis para e :
-
I.
e são iguais. E neste caso também há três possibilidades para e .
-
a)
Se e são iguais, então os três planos são iguais. POSIÇÃO 1.
-
b)
Se e são paralelos. POSIÇÃO 2.
-
c)
Se e são secantes. POSIÇÃO 3.
-
a)
-
II.
e são paralelos. Como acima esgotamos todas as possibilidades com dois planos iguais, não precisamos considerar esta opção aqui.
-
a)
Se e são paralelos. POSIÇÃO 4.
-
b)
Se e são secantes. POSIÇÃO 5.
-
a)
-
III.
e são secantes. Agora só precisamos considerar três planos secantes, pois as outras duas posições relativas possíveis já foram consideradas. Seja a reta de interseção dos planos e . São três as posições relativas possíveis de e .
-
a)
. POSIÇÃO 6.
-
b)
paralela a . POSIÇÃO 7.
-
c)
secante a . POSIÇÃO 8.
-
a)
Na disciplina álgebra linear, você vai aprender a resolver sistemas lineares de três equações com três variáveis. Cada equação deste tipo representa um plano no espaço. Lá você entenderá que existem exatamente 8 tipos de soluções possíveis para um sistema como esse pois cada uma delas representa as posições relativas dos três planos.
Exercício 4.
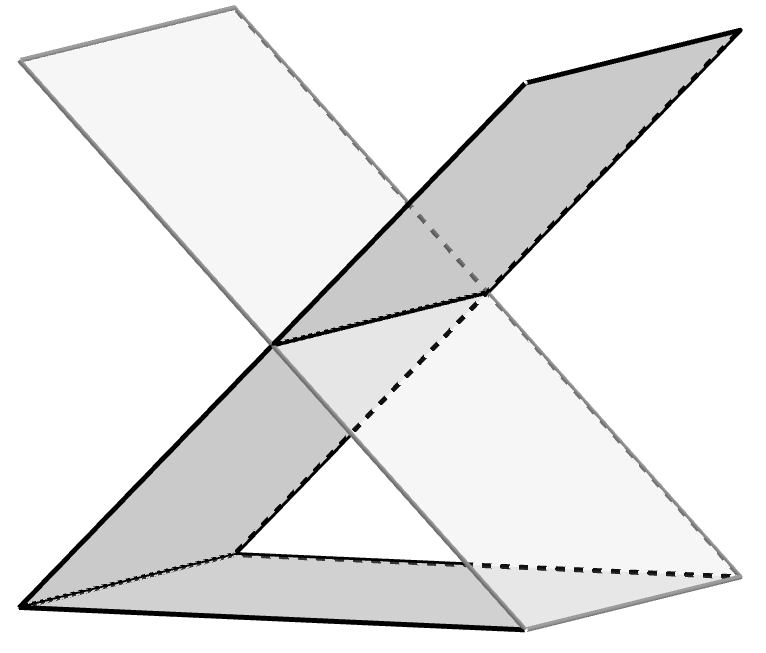
A figura a seguir representa um octaedro regular. Isto é, um poliedro formado por 8 triângulos equiláteros.
É possível mostrar que os quadriláteros , e são losangos (a parte delicada é mostrar que são polígonos planos, veremos isso na próxima aula). Mostre que os planos e são paralelos.
Solução: Os planos e são paralelos porque o primeiro possui um par de retas concorrentes que são paralelas ao outro plano (Proposição 1, da Aula 19). De fato, as retas e são concorrentes pois ambas contêm o ponto . Além disso, elas são paralelas ao plano porque não estão contidas neste plano e são paralelas às retas e do plano (Proposição 5 da Aula 18). Observe que para garantir que e são paralelas usamos que todo losango é um paralelogramo (possui os lados opostos paralelos). Analogamentte, usamos que é um losango para garantir o paralelismo de e .