Geometria Espacial - EP Aula 19
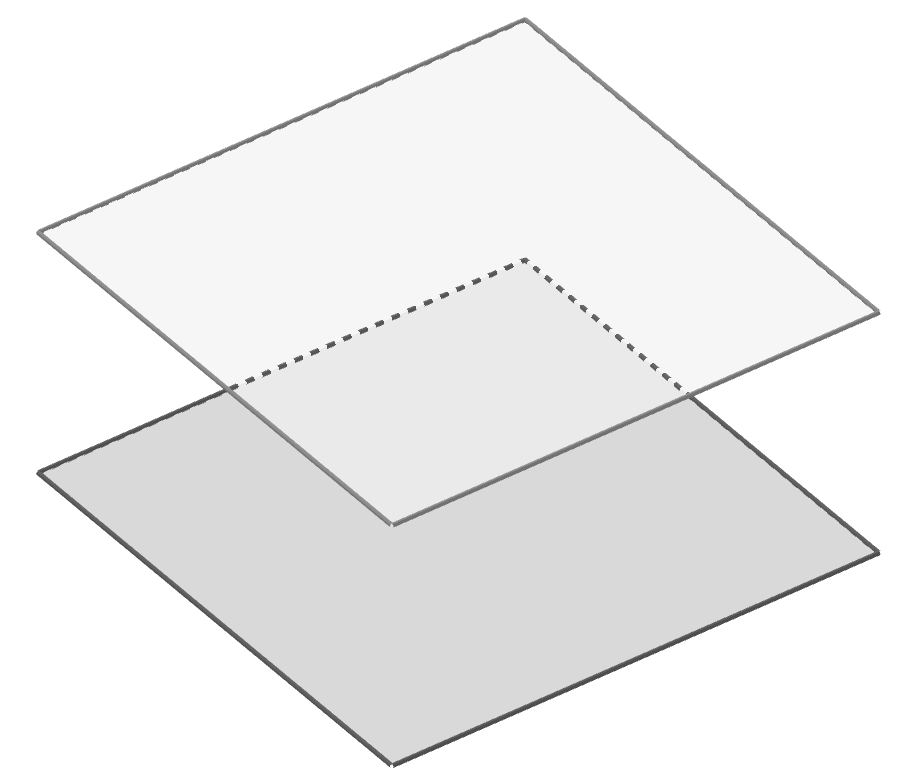
Definição: Dizemos que dois planos são paralelos quando a interseção entre eles é vazia.
Exercício 1.
A afirmação a seguir é falsa. “Se um plano contém duas retas paralelas a outro plano, então estes dois planos são paralelos.”
-
a)
Apresente um contra-exemplo com uma figura bastante ilustrativa.
-
b)
Discuta que alteração deve ser feita na afirmação para corrigi-la.
Exercício 2.
A seguir são apresentadas afirmações e justificativas para as mesmas sobre o cubo da figura. Decida se as justificativas são válidas ou não. Corrija as justificativas erradas.
-
a)
Os planos e são paralelos porque as faces e do cubo não se intersectam, isto é, as faces não têm pontos em comum.
-
b)
Os planos e são paralelos porque as retas e são paralelas, já que é um quadrado. Se um plano contém uma reta paralela a outro plano, então esses planos são paralelos.
Exercício 3.
A figura a seguir representa um octaedro regular. Isto é, um poliedro formado por 8 triângulos equiláteros.
É possível mostrar que os quadriláteros , e são losangos (a parte delicada é mostrar que são polígonos planos, veremos isso na próxima aula). Mostre que os planos e são paralelos.
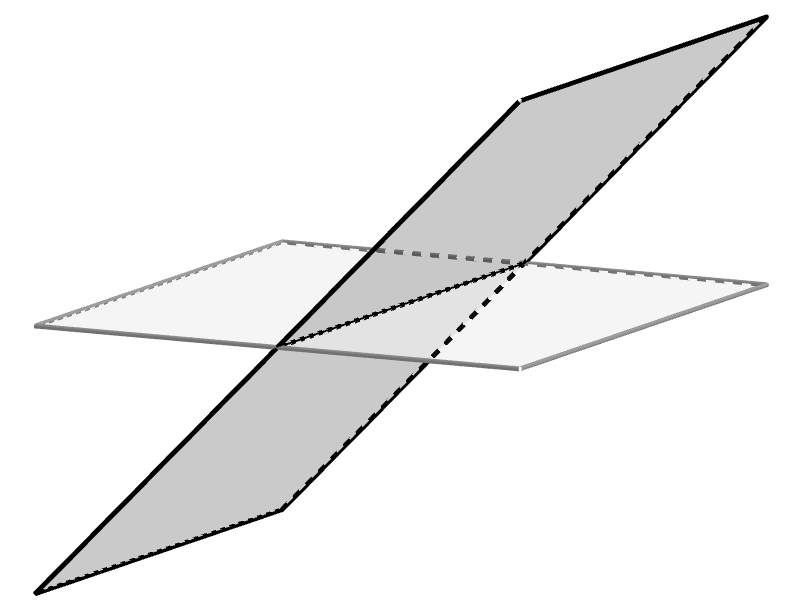
Lembre-se que dois planos no espaço podem ser secantes, paralelos ou coincidentes (quando são iguais). Estas são as posições relativas de dois pontos com relação à natureza da interseção dos planos.
Exercício 4.
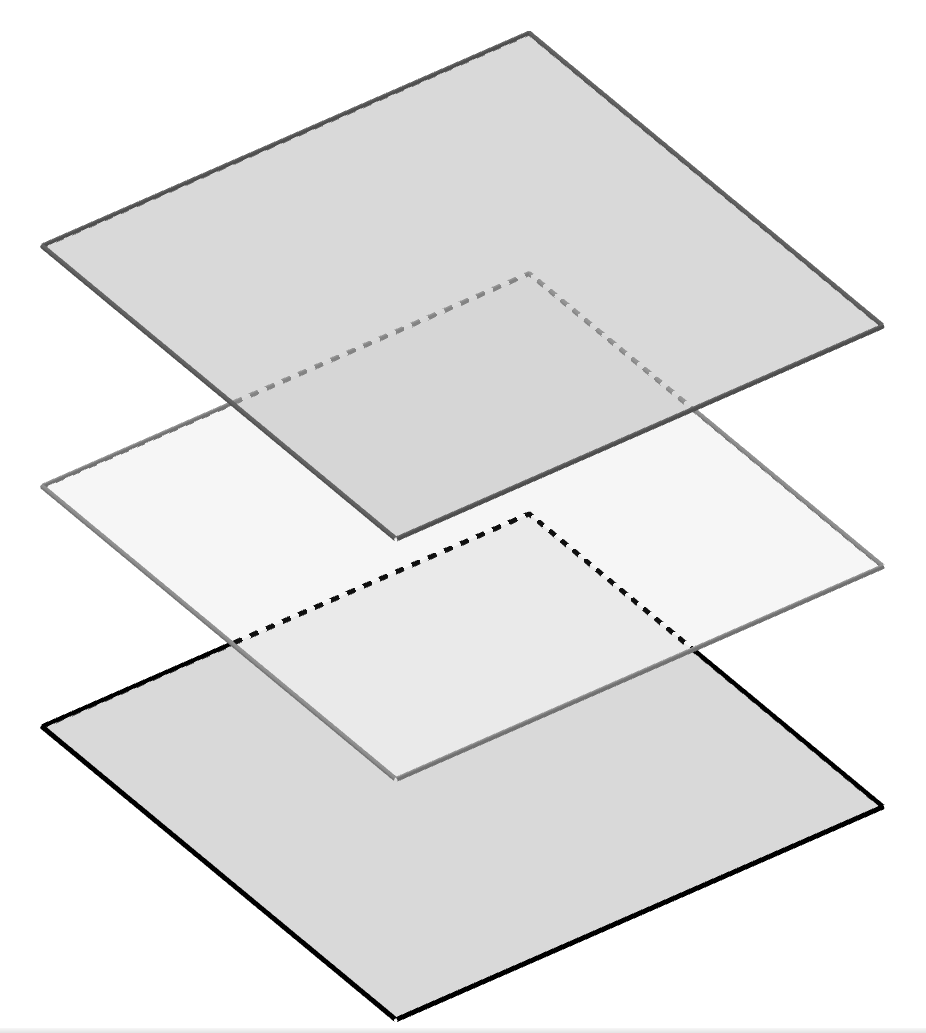
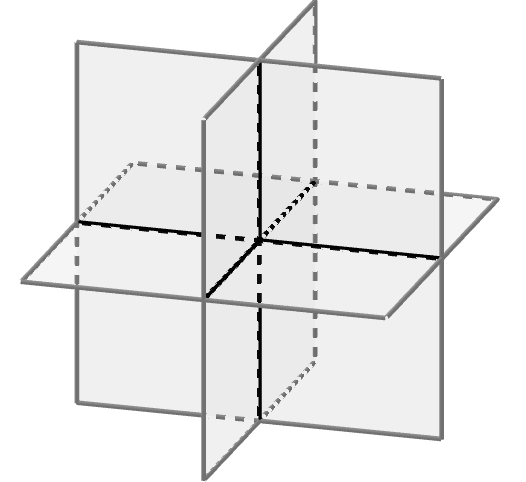
Complete a tabela a seguir com as oito posições relativas de três planos, digamos , e , no espaço tridimensional com relação às interseções dois a dois e dos três planos.
Explique com as suas palavras por que estas são todas as posições relativas com relação às interseções.