Geometria Espacial - EP Aula 18 - Gabarito
Exercício 1.
Considere três pontos , e , distintos dois a dois. Qual é o maior número de retas que eles podem determinar? Justifique.
Solução: Dizemos que três pontos são colineares quando existe uma reta que contém os três. É claro que dois pontos são sempre colineares. No caso de três pontos colineares há apenas uma reta que contém os três pontos porque duas retas que se intersectam em dois pontos são a mesma reta.
Caso os três pontos sejam não colineares, então eles formam um triângulo e o maior número de retas que eles determinam é três (combinação de 3 tomados 2 a 2). Isso porque cada dois pontos determinam exatamente uma reta. Neste caso as retas são , e .
Exercício 2.
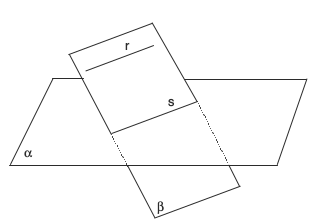
As retas determinadas pelos lados de um triângulo intersectam um certo plano em três pontos distintos. Mostre que esses três pontos são colineares.
Solução: Sejam o plano dado e o plano determinado pelo triângulo. Os pontos de interseção das retas que contêm os lados do triângulo com o plano pertencem tanto ao plano como ao plano . Logo são pontos colineares pois estão na reta de interseção dos planos e .
Exercício 3.
Considere quatro pontos , , e , distintos dois a dois. Qual é o maior número de retas que eles podem determinar? Justifique.
Solução: Como buscamos o maior número de retas que esses quatro pontos determinam, devemos tomar quaisquer três como sendo não colineares. Neste caso, cada par de pontos distintos vai formar uma reta. Teremos 6 retas distintas (combinação de 4 tomados dois a dois): com temos , e , com temos , e , mas . Com temos , e , mas e . Finalmente, as retas são , , , , e .
Exercício 4.
Considere quatro pontos , , e , distintos dois a dois. Qual é o maior número de planos que eles podem determinar? Justifique.
Solução: Três pontos são sempre coplanares e neste caso eles determinam no máximo um plano, caso eles sejam não colineares. Mas 4 pontos podem ser não coplanares e, neste caso, cada três determina um único plano, portanto, tomando as combinações de 4 tomados 3 a 3 obtemos 4 planos distintos. Outra alternativa, sem utilizar técnicas de contagem é listar todos os planos: , , e .
Exercício 5.
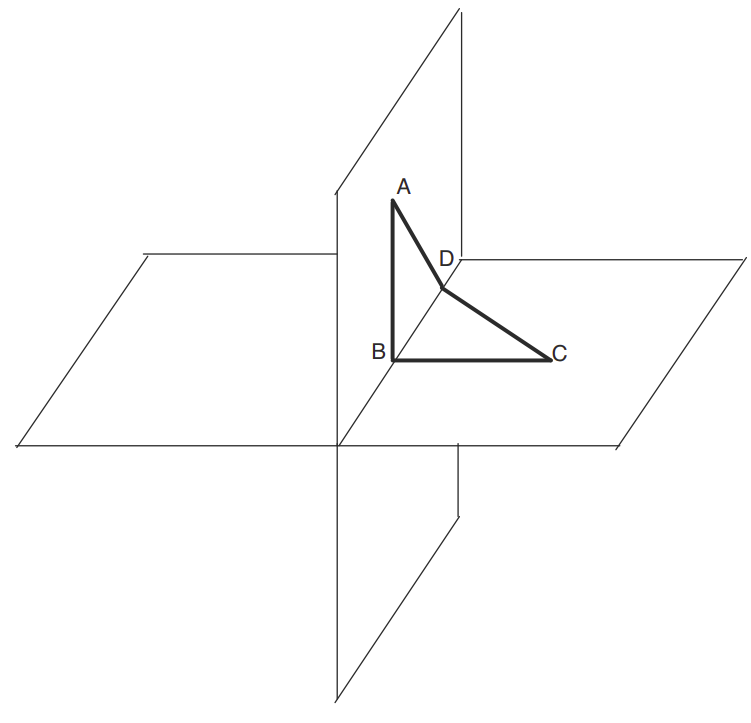
Desenhe um quadrilátero reverso, isto é, um quadrilátero com arestas opostas contidas em retas reversas.
Solução: Uma possibilidade é a da figura a seguir.
Exercício 6.
Dada uma reta , mostre que existem infinitos planos contendo .
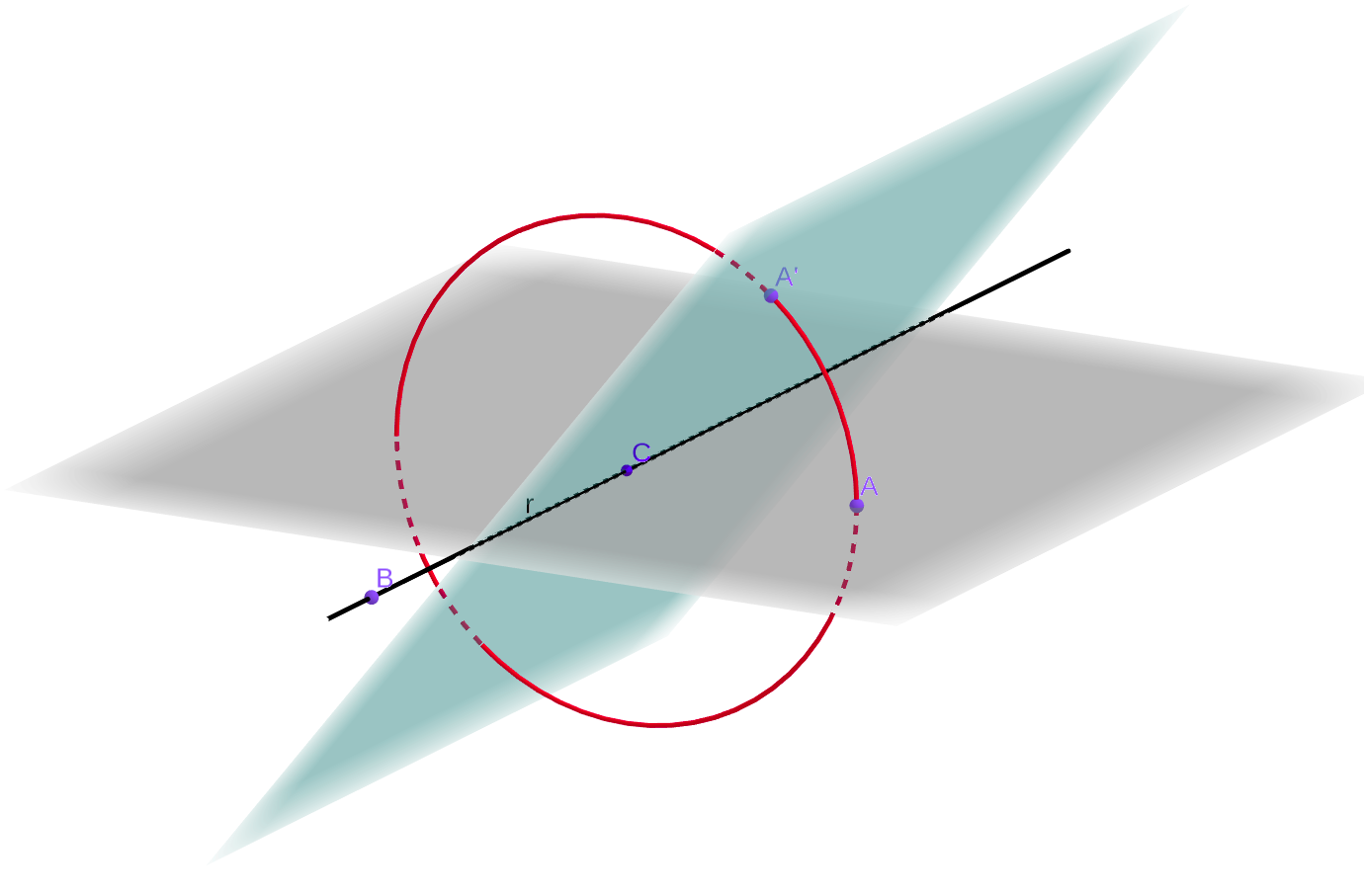
Solução: Sejam e pontos de e um ponto externo a . Considere uma circunferência de centro em que passe por . Para cada ponto de , os pontos , e são não colineares porque , logo determinam um plano . Além disso, cada ponto de , determina um plano distinto. De fato, se pertencem a , então o plano contém apenas se for o ponto de diametralmente oposto a .
Mova o ponto no aplicativo do GeoGebra para ganhar intuição à respeito (link).
Exercício 7.
Você leciona em uma escola do Ensino Médio e durante uma atividade em sala de aula um estudante afirma que “duas retas são reversas quando estão em planos paralelos.”. Argumente para mostrar ao estudante que ele está errado e, além disso, para que ele entenda o que são retas reversas. Use a imagem de um cubo para ilustrar.
Solução: Duas retas são reversas quando não existe um plano que contenha as duas, isto é, quando não são coplanares. Quando duas retas são reversas, existe um (e somente um) par de planos paralelos tais que cada plano contém uma das retas. Mas retas contidas em planos paralelos também podem ser paralelas entre si. Por exemplo, no cubo , as retas e são reversas pois o único plano que contém , e é a face e esse plano não contém o ponto . Por outro lado, as retas e estão contidas nos planos paralelos e , respectivamente, e são paralelas.
Exercício 8.
Decida se as afirmações a seguir são verdadeiras ou falsas. Prove as verdadeiras e encontre um contra-exemplo para as falsas (este contra-exemplo deve ser descrito e desenhado. Não vale só desenhar, tem que explicar o porque é trata-se realmente de um contra-exemplo).
-
a)
Por três pontos distintos passa um único plano.
-
b)
Se três retas passam pelo mesmo ponto, então essas retas são coplanares.
-
c)
Por dois pontos distintos passam infinitos planos.
-
d)
Quatro pontos não coplanares determinam quatro planos.
-
e)
Se uma reta não contida num plano é paralela a uma reta do plano, então ela é paralela ao plano.
-
f)
Se duas retas distintas são paralelas a um plano, então elas são paralelas entre si.
Solução:
-
a)
Falsa. Caso os três pontos sejam colineares, por eles passarão infinitos planos. Veja a figura do Exercício 4.
-
b)
Falso. As três arestas em um vértice de um cubo, estão contidas em três retas que se intersectam em um ponto, mas não são coplanares.
-
c)
Verdadeiro. Veja a solução do Exercício 4.
-
d)
Verdadeiro. Esta é uma maneira de expresssar em uma única frase as Proposições 4 e 5 da Aula 18. Sejam uma reta não contida no plano e uma reta de tal que e são paralelas. Queremos mostrar que , argumentaremos por contradição. Se existe , vamos mostrar que , o que é uma contradição pois as retas e são paralelas, donde concluiremos que . Considere o plano determinado pelas retas paralelas e . Os planos e são secantes pois não são iguais ( não está contida em ) e não são paralelos ( está na interseção dos dois planos), assim a interseção de e é a reta . Ora, se , então . Logo .
-
e)
Falso. Considere dois planos paralelos e um par de retas concorrentes em um deles.