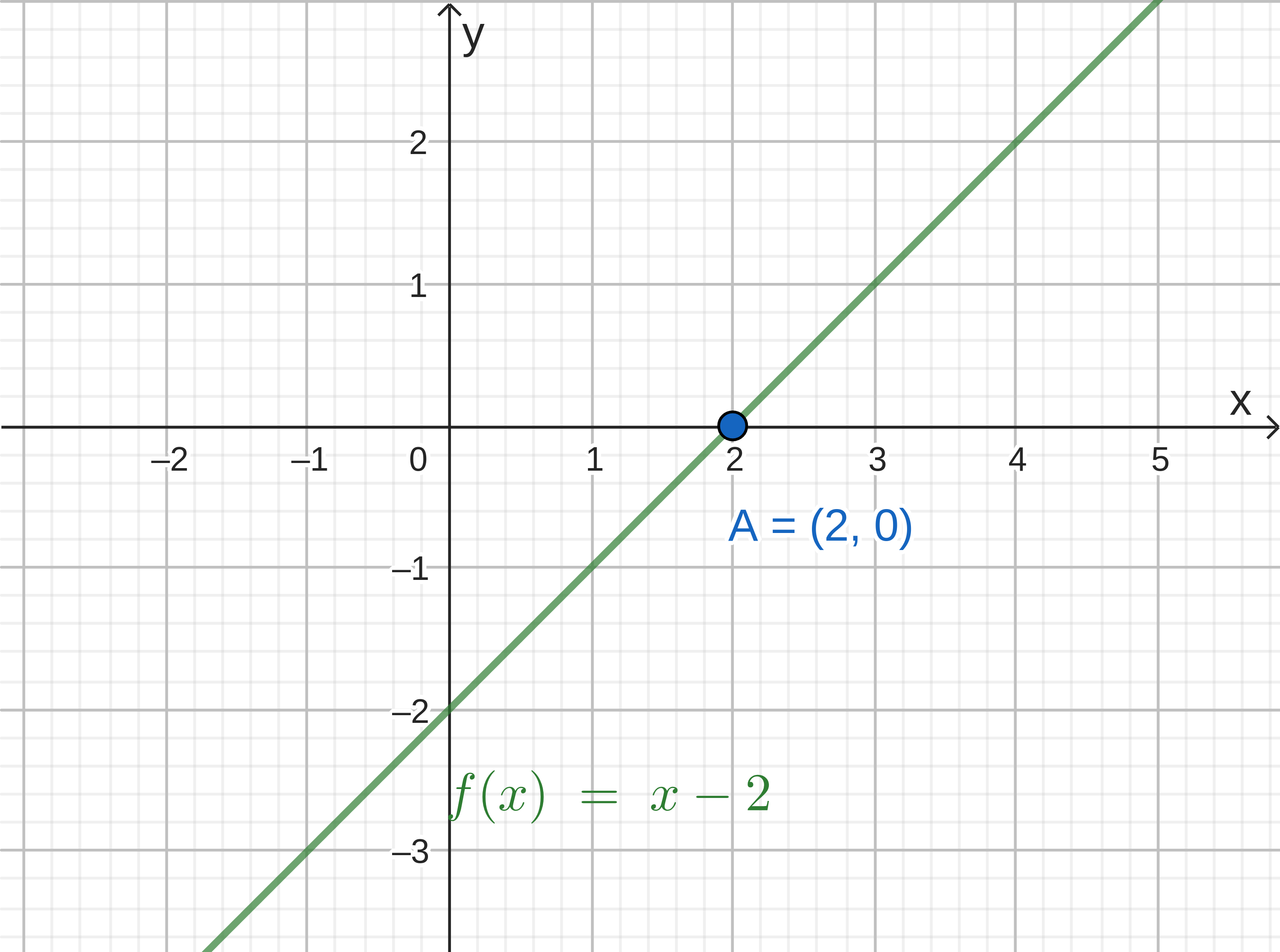Registre suas dúvidas neste canal.
Seja membro do nosso servidor por meio deste link. Sendo membro você pode participar de áudio ou videotutorias e receber nossos comunicados.
Para saber quando terão tutorias presenciais, acesse este link para entrar no grupo de comunicações.
Se nada funcionar, você sempre pode procurar o Profº Simas por e-mail fabio.simas@uniriotec.br.
Esta aula é continuação da anterior. Alguns dos conhecimentos lá desenvolvidos serão usados aqui.
O principal objetivo de aprendizado desta aula é:
Definição: Dada uma função real f, dizemos que um elemento do domínio, digamos x = a, é uma raiz (ou um zero) da função f quando f(a) = 0. Portanto, as raízes da função f são as soluções da equação f(x) = 0, em que x pertence ao domínio.
Exemplos:
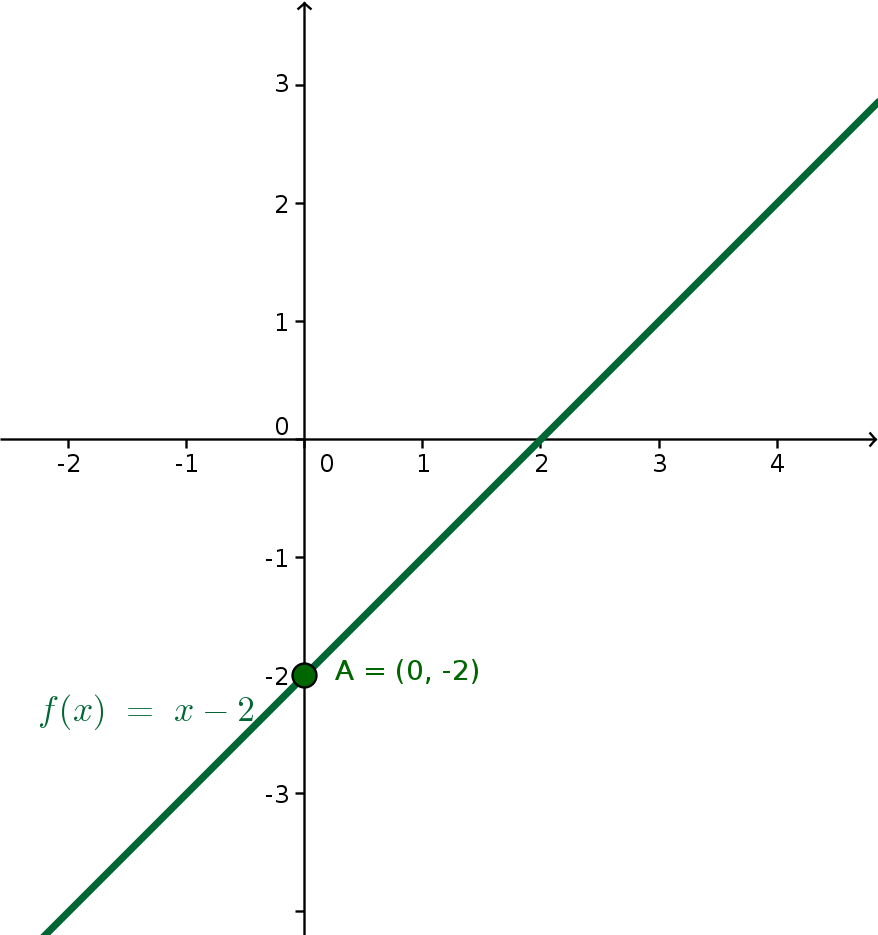
a) f(x) = x - 2. A função f tem uma raiz em x = 2, afinal f(2) = 2 - 2 = 0.
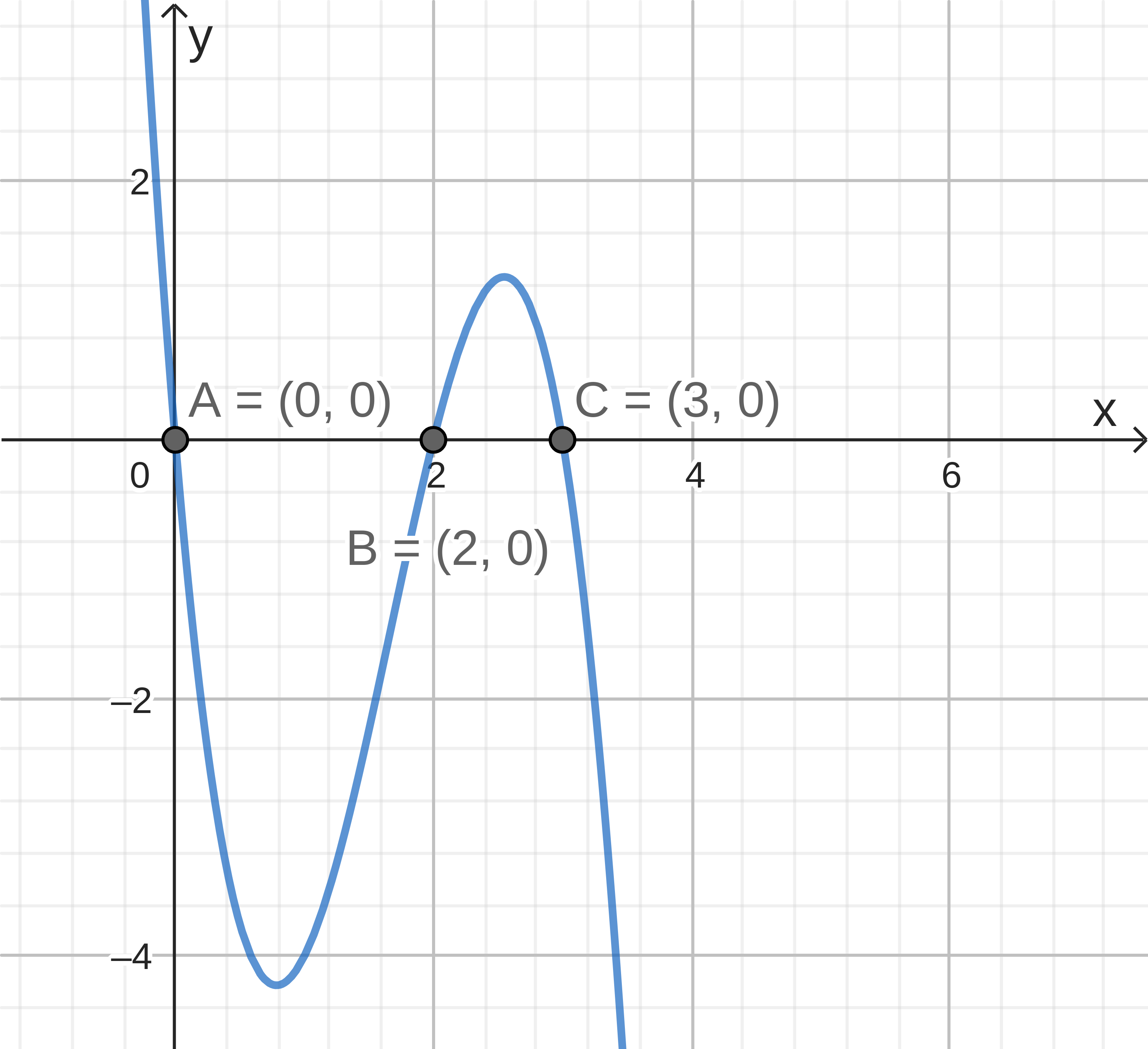
b) g(x) = x(x-2)(6 - 2x). A função g tem três raízes, em x = 0, x = 2 e x = 3. Afinal, g(0) = 0.(0 - 2).(6 - 2.0) = 0, também g(2) = 2.(2 - 2).(6 - 2.2) = 0 e g(3) = 3.(3 - 2).(6 - 2.3) = 0.
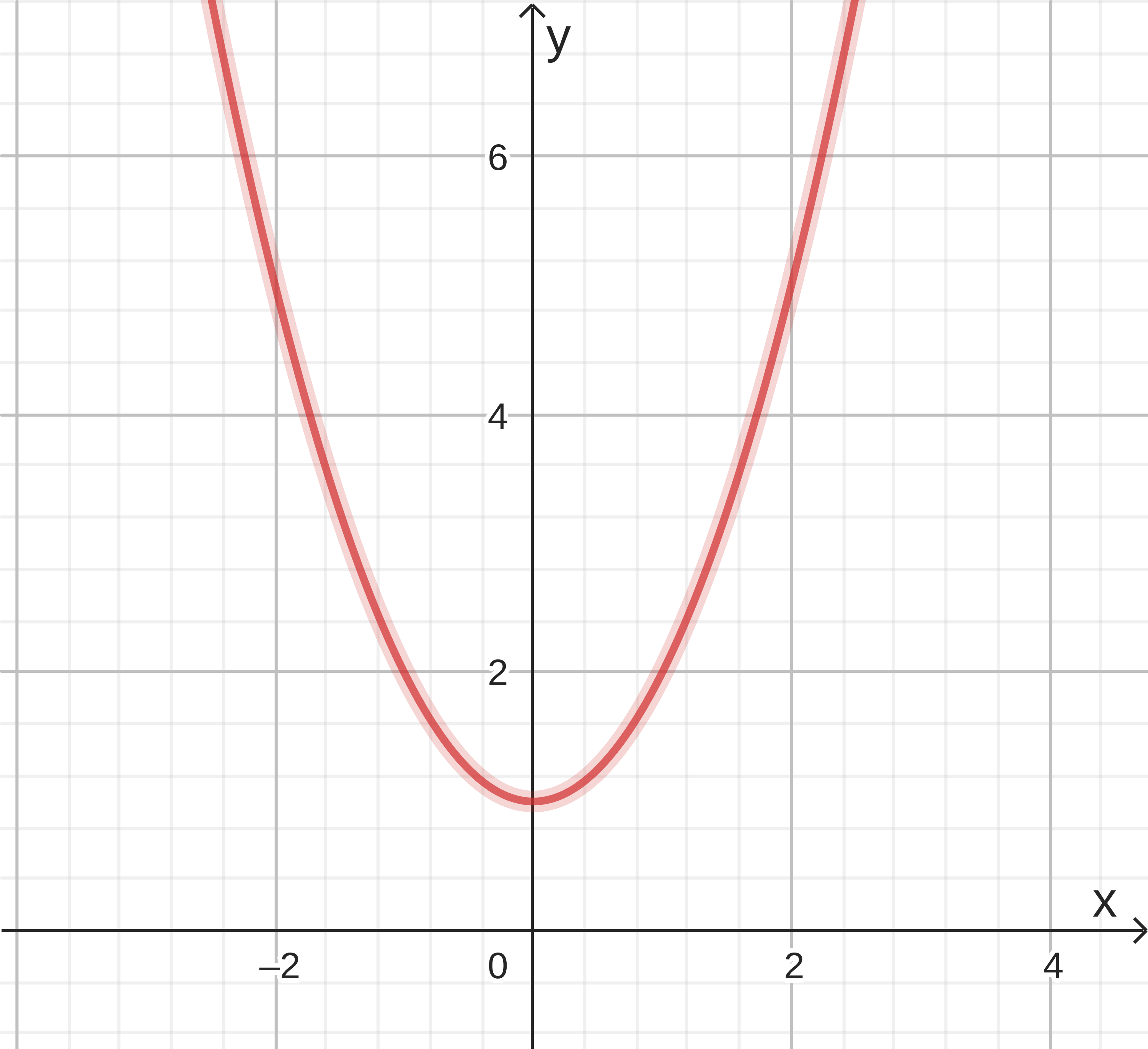
c) h(x) = x² + 1. A função h não tem raiz real, pois não existe número real x tal que x² + 1 = 0.
Observação: Nem sempre é fácil calcular a raiz de uma função dada sem usar uma calculadora.
Representação gráfica. Lembre-se que os pontos do gráfico de uma função são aqueles do tipo (x , f(x)), onde x pertence ao domínio da função. As raízes (ou zeros) de uma função f são os pontos 'a' tais que f(a) = 0. Então as raízes correspondem aos pontos do gráfico que têm segunda coordenada igual à zero, isto é, são os pontos do tipo (a , 0) do gráfico da função. São os pontos em que o gráfico intersecta o eixo x. Veja os exemplos:
a) f(x) = x - 2. Como vimos, x = 2 é a raiz de f, então sua representação no gráfico é o ponto A = (2 , 0).
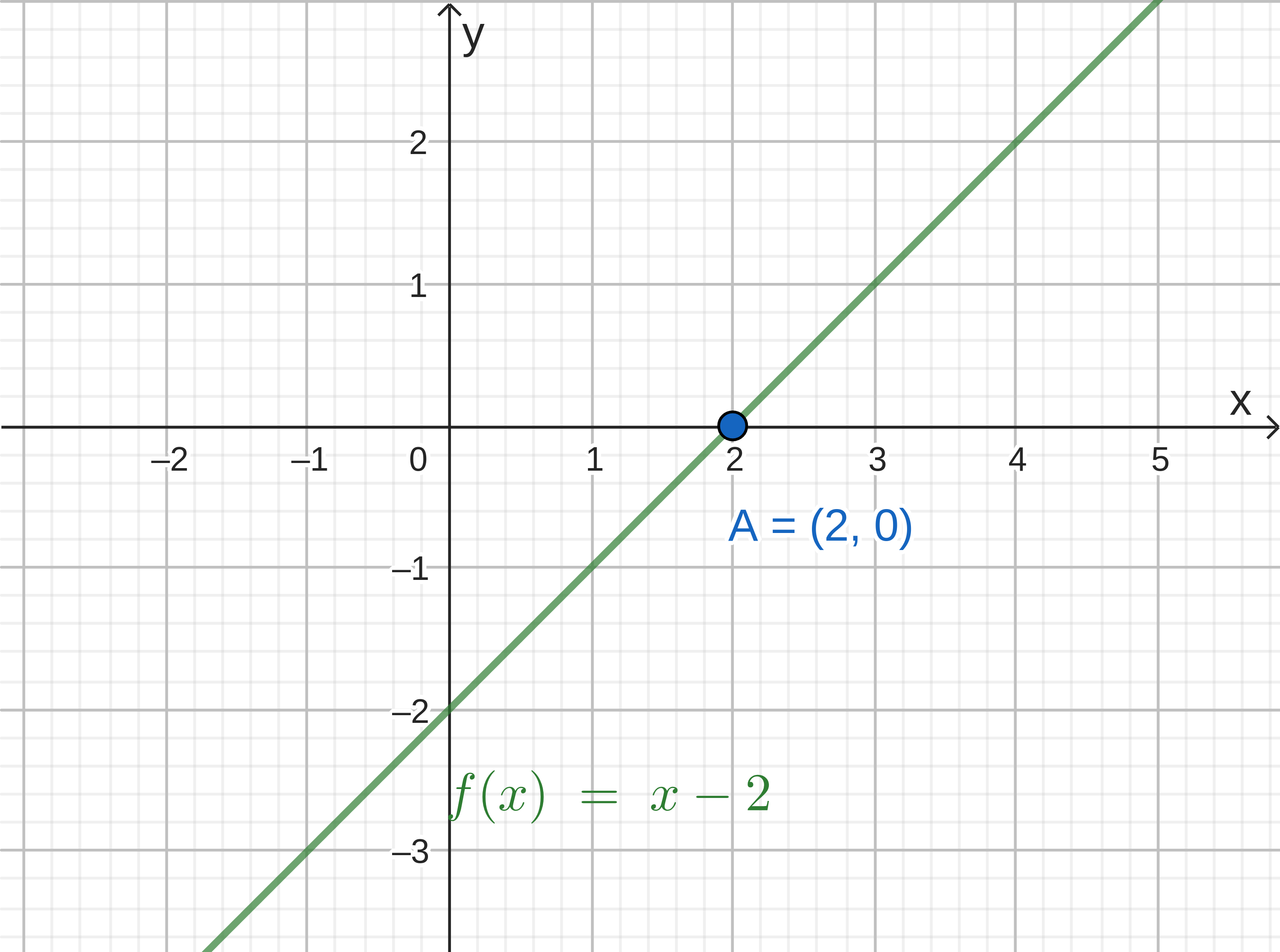
b) g(x) = x(x-2)(6 - 2x). As raízes de g são x = 0, x = 2 e x = 3. Suas representações gráficas são os pontos A, B e C na figura.
c) h(x) = x² + 1. Como vimos, a função h não tem raiz real, logo seu gráfico não intersecta o eixo x.
Definição: Dada uma função real f em que o número zero pertence o domínio de f, dizemos que um número b é o intercepto-y da função, quando f(0) = b.
Observação: Graficamente, se b é a imagem de zero, então o ponto (0 , b) pertence ao gráfico de f e é o ponto em que o gráfico da função intersecta o eixo y.
Exemplos:
a) f(x) = x - 2. O intercepto-y é f(0) = 0 - 2 = -2.
b) g(x) = x³ - x² + 4. O intercepto-y é g(0) = 0³ - 0² + 4 = 4.
c) h(x) = 1/x. O número zero não pertence ao domínio da função h, pois não existe divisão por zero. Essa função não tem intercepto-y.
As definições e imagens a seguir foram adaptadas do capítulo Introdução às Funções do Livro Aberto de Matemática (IMPA/OBMEP), de autoria dos prof. Michel Cambrainha e Gladson Antunes (UNIRIO).
Definição: Uma função \(f\) é dita crescente em um intervalo \(I\) do seu domínio, quando os valores das imagens, \(f(x)\), aumentam à medida em que os valores de \(x\) aumentam dentro do intervalo, ou seja, para todo \(x_1,x_2\in I\), \(x_1<x_2\) implica \(f(x_1)<f(x_2)\).
Definição: Uma função \( f \) é dita decrescente no intervalo de números reais \(I\), quando os valores das imagens, \(f(x)\), diminuem à medida em que os valores de \(x\) aumentam em \(I\), ou seja, para todo \(x_1,x_2\in I\), \(x_1<x_2\) implica \(f(x_1)>f(x_2)\).
Definição: Uma função \( f \) é dita constante no intervalo de números reais \(I\), quando os valores das imagens, \(f(x)\), não se alteram à medida em que os valores de \(x\) mudam em \(I\), ou seja, existe um número real \( c \) tal que para todo \( x \in I \), implica \(f(x) = c\).
Mova os pontos azuis até que \( I \) seja um intervalo em que a função é crescente.
Mova os pontos vermelhos até que \( J \) seja um intervalo em que a função é decrescente.
Mova os pontos púrpura até que \( K \) seja um intervalo em que a função é constante.
Depois confira a sua resposta clicando em "Conferir".
Clique nos links para trocar a função.
Função 1, Função 2, Função 3, Função 4